You have to wonder why Jonathan only talks about p values and hides the fact that for his p values to be significantly low the temperature trend must be huge, much larger than the climate change trend.
This he is insinuating that the reason why I use p values is because it is very rare to find a significant increase in temperature and thus by it's own lack of power, rejects any sense of global warming.
Firstly, even if that were true (which is isn't), there is nothing wrong with that. We do need statistical proof that we are heating up at all the right times.
And secondly, this is completely false, and I decided to prove it (as I have actually done to count before but he obviously refuses to recognise it).
I decided to do 1000 simulations of 100 years of data of which the temperature rises from 16 degrees to 16.6 degrees - which is about the so called norm. Using a standard deviation of 0.5, which I found to be fair and, if anything to over exaggerate the variability in climate the temperature should increase slowly from 16 to 16.6.
Here is an example of one the graphs that was produced. Note the slight gradual increase in temperature, although there seems to be no major increase in the last 75 years according to this graph. But as I said this is one of a thousand that I simulated.
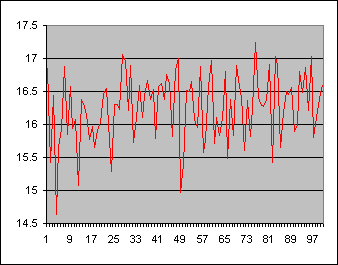
Incidentally, the graph above showed a significant increase in temperature (t = 2.2, p = 0.03).
But after simulating this 1000 times, I found that 811 of the 1000 simulations were highly significant (p value less than 0.01), and that 941 of the simulations were significant (p value less than 0.05). This meaning that 59 of the simulations were not significant - or about 6%
If you knew anything about statistics, this is exactly as what we would expect given that the null hypothesis was false, about a 5% false negative (in this case 6%).
Of course this also proves another thing, in that using p values for determining whether an increase in temperature is perfectly adequate.
And it also proves that Count Iblis was completely and uterrly wrong.
And it also proves that Count was keen to tell the world that the method of statistics that I use was wrong (which it isn't) when he had absolutely no proof whatsoever.
And it also proves that Count wrongly attempted to discredit the statistical analysis of this website without the obvious statistical proess.
And it also proves that if someone proves something that goes against what Count believes in he will turn to conspiracy theories.
And lastly, it proves, that Count will believe in anything, anything that agrees with his own personal zeitgeist, but the minute someone suggests something else he will attempt to discredit rather than do the scientific thing which is to engage in rational debate and attempt to find the truth.
In summary, the Count has proven he is no scientist. Unfortunetley, this religious type attitude, is the reason why climate science is being held down.
4 comments:
I have no problems to admit that I'm wrong, if in fact this is the case.
Why don't you give a p value for no deviation deviation from the average global warming trend instead of a p value for no trend?
You can say that you can detect the climate change signal in simulated data over 100 years, but the data you analyzed don't go back that long. So, one would expect that the confidence intervals would be larger in those cases...
Anyway, why not give confidence intervals for the trends and then tell if the expected climate change signal is inside or outside this interval?
I could give p values for the deviation from the average global warming trend, but this in itself would prove nothing. There is nothing wrong with not finding a significant result.
In fact the results will be exactly the same as given in this article. A simulation of it would show the exact same thing. that 94% of cases were significantly less than 0.6 degrees per century.
Confidence intervals are not necessary when you have a p value. They go hand in hand, but a true scientist would be interested moreso in p values than confidence intervals.
Also, you did request this on another forum, of which I replied and proved it to you. So why ask again?
Confidence intervals are indeed not necessary, but it does matter for another purpose: To communicate your results to the scientific community in a transparant way.
If you just say that "I detected no significant change", then I have to dome some effort to find out to find out if that means that some theory that predicts change is now ruled out. If you just give the confidence inteval, and the predictions of the theory are outside your confidence interval, then I can see that at one glance.
I disagree with your statement that true scientists are moe interested in p values. Of course not, because p values depend on the specifics of your study (how much data you've sampled etc.).
But the confidence interval is a statement about the real world, in this case about how large temperature trend can be. The temperature trend is a quantity of interest to climate scientists. A statement like: "No change is within my 95% confidence interval" is completely useless to a climate scientist.
A couple of questions.
First, your 1000 simulations... I assume this is a model, rather than a form of resampling? If so, do your model series display similar spectral characteristics to real temperature data?
Without knowing how you did your modelling, its really very hard to say whether you proved anything. So how did you generate your model series? Can you tell the difference between the population of these modelled series for different temperature changes?
Second, confidence intervals are very useful. As a professional scientist (and I would imagine that would mean I count as a true scientist) I find that confidence intervals are often more instructive than probabilities alone. Especially when showing uncertainties across a whole data set.
Third, isn't a question... I'd actually like to refer you to a paper you may find interesting.
Lobell, D. B., C. Bonfils, and P. B. Duffy (2007),
Climate change uncertainty for daily minimum and maximum
temperatures: A model inter-comparison, Geophys. Res. Lett., 34,
L05715, doi:10.1029/2006GL028726.
Post a Comment